Nanda Syahrasyad

Last updated November 13, 2021

The simple array is probably the most popular data structure in programming. It's a straightforward yet powerful tool — it lets you represent an ordered list of items with fast random access. It doesn't matter if you're looking for index 1 or index 500 — with the array, both accesses take the same amount of time.

If you've been a developer for a while, you probably use arrays on a daily basis without thinking too much about them. But have you ever wondered how arrays actually work?

In this post, I want to dive into the technical details of the array and figure out how you might invent the array yourself. We're going to start with a simple array that only supports numbers, then later build that up to the flexible, dynamic array we all know and love from JavaScript.

Let's get started!

Memory API

To implement our array, we'll use our computer's memory API (or a super simplified version of it). This API has four methods:

1. get(address: number) — returns the value at a specific memory address.
2. set(address: number, value: number) — sets the given address to the given value.
3. allocate(bytes: number) — allocates a given number of bytes, returning a pointer to the first allocated byte.
4. free(pointer: Pointer) — frees the memory location pointed to by the pointer.

If you've written code in a lower level language before, some of these methods might be familiar to you; if not, that's okay too — we'll go over how everything works in this section.

Reading, Writing, and Addresses

As a starting point, you can think of memory as itself a super long array, where each element of the array represents a single byte:

You can refer to specific bytes in memory using their address — just like how you can use an index to refer to specific elements in an array.

Memory Allocation

One key restriction behind our computer's memory system is that you can't freely read and write to any old address in memory*. In fact, when you begin, you can't read and write to any address at all!

*And for a good reason too — your computer memory is shared between the hundreds of different programs running in parallel. Imagine if programs can change memory that's being used by other programs!

To get past this restriction, you have to ask for space in memory by allocating it. To allocate space, you use the allocate function, passing in the specific number of bytes that you need:

The allocate call returns the address of the first byte of the allocated block. In this case, the call returns the address 0 because our 2-byte block begins at address 0.

Great! Now that we have our allocated slice of memory, we can read and write from it as we please:

Notice how we weren't allowed to write to block + 2 - that's because we only allocated 2 bytes, so the third byte, block + 2, is out of bounds!

Freeing Up Space

Finally, once you're done with the data and don't need it anymore, you can free up that space so the computer can use the memory for other things:

const pointer = Mem.allocate(/* num of bytes */ 12)

// do stuff

Mem.free(pointer)

One thing you might notice from this allocate-free workflow is that you end up not referencing addresses directly. Instead, these addresses live inside variables, and all you need to do is move them around. Overall, the typical memory management workflow looks like this:

// Allocate
const block = Mem.allocate(3)

// Use
Mem.set(block, 'a')
Mem.set(block + 1, 'b')
console.log(Mem.get(block)) // prints 'a'

// Free
Mem.free(block)

As a quick summary:

• Memory, for our purposes, is a long array of bytes where each byte has an associated address.
• To use memory, you need to allocate it first; this allocation process returns the address of the first byte of the allocated block.
• Once allocated, you can freely read and write to that memory location.
• When you're done, you can free the allocated space so it can be used elsewhere.

Building the Array

Now that we know a bit about memory and how it works, let's get on with our array! We'll start with a few assumptions to make our lives easier:

1. The array has a fixed length (i.e. it cannot grow in size), and
2. The array can only contain numbers.

These assumptions may seem really restrictive, but don't worry — we'll ease them as we move on.

Allocating Space

The first thing that we need to do is allocate space for our array. But, how much space?

const data = Mem.allocate(/* num of bytes */ ???)

Thankfully, our assumptions let us determine the size of our array ahead of time. Since our array is a fixed length and can only contain numbers, the total number of bytes we need to allocate is:

total # of bytes = length * (# of bytes for 1 number)

For the number of bytes for 1 number, we'll use JavaScript's size of 8 bytes. This means that if we want to allocate an array of 10 numbers, we would need to allocate 10 * 8 = 80 bytes in total.

Reading and Writing

Next up, we'll need to implement the reading and writing operations so our array is actually usable:

arr.set(/* index */ 0, /* value */ 2)
const item = arr.get(/* index */ 0) // item = 2

Remember that the core property of the array is fast random access. This means retrieving the element at index 500 should take as long as retrieving the element at index 1. This leads us to our problem:

Keep in mind that, given an address, your computer's memory can quickly fetch the item at that address. If we're able to efficiently translate an index to a memory address, we'll be able to quickly retrieve the element located there.

Let's work through this using an example. Say we have an array with three numbers, each 2 bytes large:

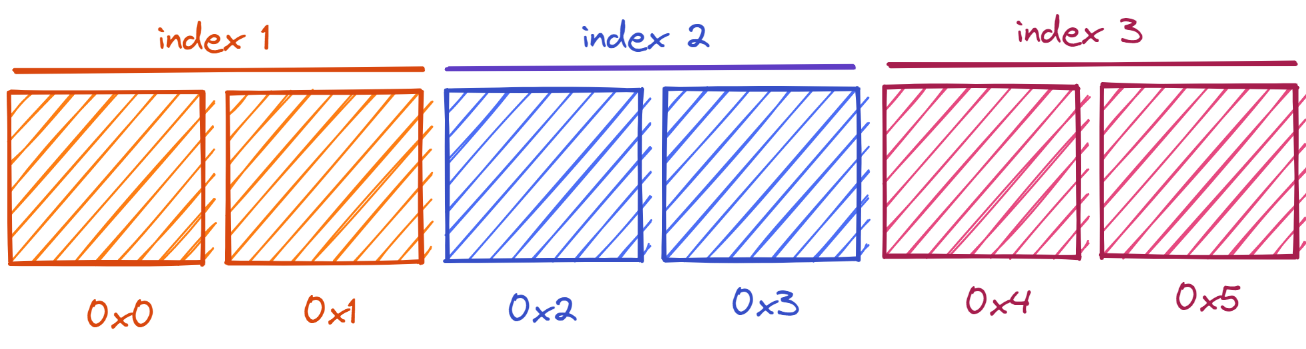
Using only the address of the first byte, how would we get the address of the element at index 0? What about index 1? Or index 2? Take a look at the diagram above and see if you can find a pattern.

We don't need to do any more work for index 0 - the address of the first byte is the address of the first element! But what about the other indices?

From the diagram above, we see that the address of the second element (at index 1) is the address of the first byte plus the size of the first element:

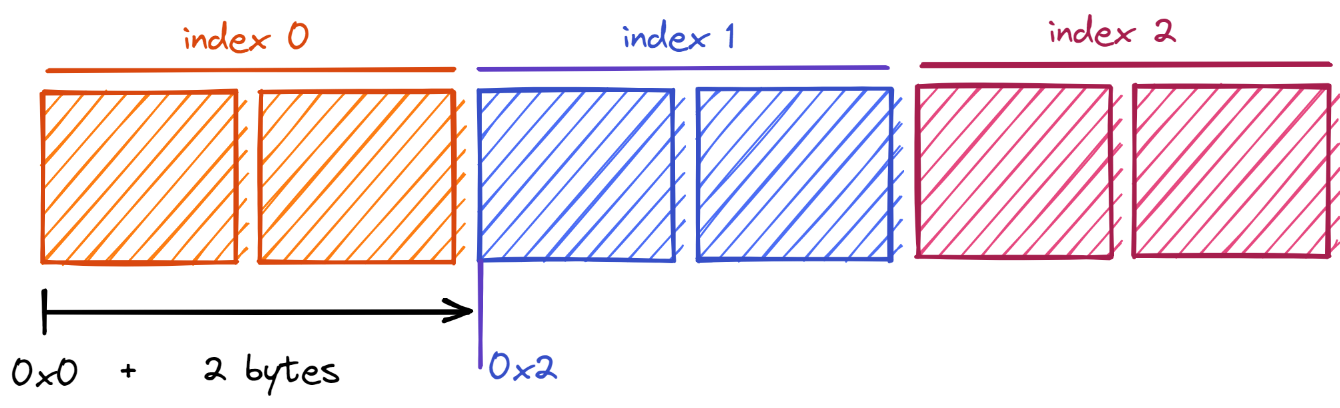
Expanding on that further, we find that the address of the second index is the address of the first byte plus twice the size of each element:

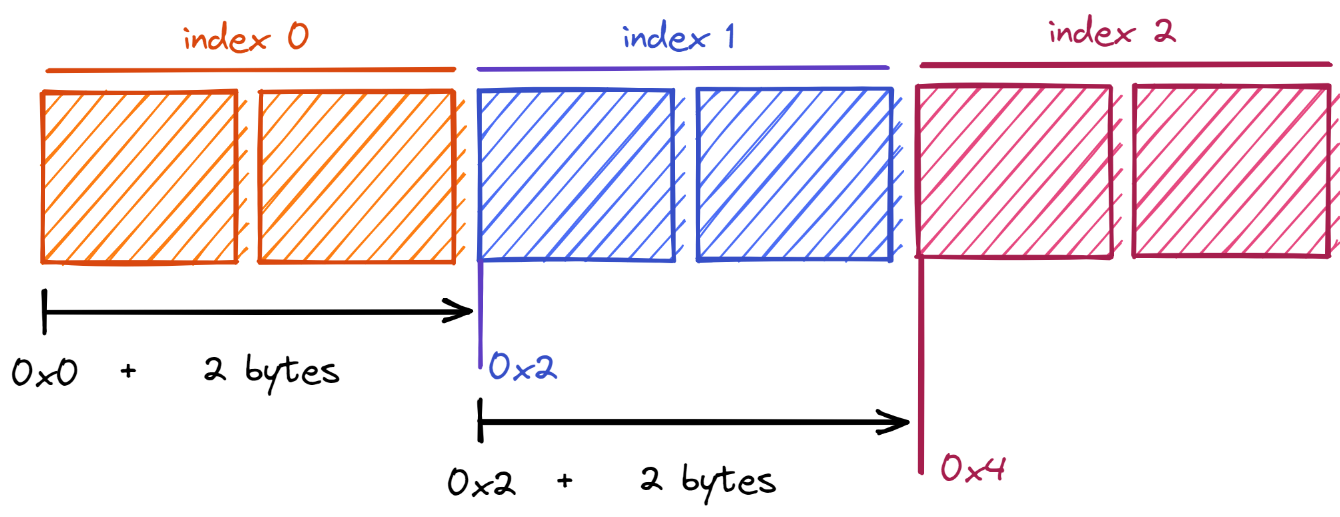
In general, the address of an element at any index can be determined with the following formula:

address = first byte address + (index * size of each element)

Once we have the address of the element, we can freely read and write to that location using the memory's get and set functions.

Something to highlight here is that it doesn't actually matter what type of data the array contains - if every element is the same size, then our formula would work fine!

Great work! We now have an array that we can use to represent data. Except, it feels a bit limiting - what if we don't know how many elements we need ahead of time? Or what if we want to store different elements in the same array?

Let's answer these questions one at a time, starting with the former - making the array dynamic.

Growing the Array

So far, our array is static. We define a length when we create it, but it can never exceed that initial length. This is pretty limiting — what if we don't know how many elements our array will contain?

In this section, we'll explore a way to make our array dynamic, making it grow and shrink as the number of items in the array change. In particular, we'll explore how to implement a push function that adds items to the end of the array.

const arr = [1, 2, 3]
arr.push(4) // adds 4 to the end of the array

A First Pass

To start, let's consider the case where our array isn't full yet, i.e. the array has fewer items than the length we initialized it with:

When we call push, we want to add the value to the end of the array, or index 2 in this case. Because this block was previously allocated, we're good to set the value at index 2 directly.

But what if we want to call push again? The end of the array points to an unallocated block, so we can't freely write our value — the memory won't let us. How do we grow our array then?

Increasing Capacity

Since we need space for more data, our solution is to allocate more memory. But, how much more memory should we allocate? One thing we might be tempted to do would be to allocate just enough memory for the new element:

This would work just fine if the array was the only thing in memory because then there's always going to be space right next to the array. In practice, though, arrays don't live in a vacuum. It's totally possible, and actually very likely, that the space around the array is occupied by something else:

In which case, you can't really be sure where the allocator will allocate your new block.

Okay, so if that doesn't work, what should we do then? Our only option is to allocate memory for the whole array plus the new element:

Next, we'll need to copy the array into the new space:

Push the new element into the extra space we now have:

And free up the old location:

And we there we have our push function!

A Note on Performance

One push call is typically followed by more push calls in actual code, so allocating more than one block of extra space is generally more performant.

This way, you won't need to resize the array again if you call push multiple times:

Mixing Types

Great work! So far, we've made an array that:

1. Can quickly find an element given an index
2. Can grow as more items are added to the array

This leaves us with one last assumption: our array can only contain the same type of data. How do we modify our array to handle any kind of data thrown at it?

The Problem

Before we look into implementing this in our array, let's try to get a better sense of the problem first. Let's say that we did allow our array to contain multiple types, and all we did to support that was to lay out the items one after another as we've always done.

Using the array ['ab', 10, true] as an example, our array might look something like this (in memory):

Now, let's say we want to get the boolean true which is located at index 2. To do this, we would plug in "2" into our address formula:

address of index 2 = address at index 0 + (size of item * 2)

But, um, wait a minute — we're missing a variable. What should we put as the "size of item"? We have three choices:

1. 2 bytes, the size of the string 'ab'
2. 4 bytes, the size of the number 10
3. 1 byte, the size of the boolean true

Turns out none of these options give us the correct answer.

If we put in 2 (using the size of the first element), our formula gives us 4 as the address; whereas the correct address is 6, since the number "10" takes up 4 bytes of space. Likewise, if we use 4, we'll overshoot the address, while if we use 1, we'll undershoot the address.

If our formula doesn't work anymore, we won't be able to quickly determine the address of any given index - the core feature of the array! Therefore...

Boxing Our Items

As it turns out, the solution is to force each element to be the same size by "boxing" them. This box will essentially act as padding so that each element ends up where you expect it to:

In the example above, we boxed each element of the array in a 4-byte container — the size of the largest of the three data types. With each element being padded to a multiple of 4, we can now use our formula to calculate the address of any particular index.

Summary

Whew. If you made it all the way here, thank you! I appreciate you. Turns out there's quite a bit happening in the background when we work with arrays. Let's summarize what we've learned:

1. Computer memory is restrictive. You can only use specific bytes by allocating memory first. Because of this, making arrays dynamic is not super straightforward.
2. Array indices get converted to a memory address. This process needs to be fast so that our array can have fast random access.
3. Adding more items to an array might mean we have to resize it under the hood. But as long as we resize correctly, we don't have to resize too often.
4. To make an array handle multiple types, we have to "box" each element in the array so that they take up the same amount of space in memory.

And that's it! Hope you've enjoyed our inventive approach to how arrays work, and thanks again for reading!